JAK1+VC
Interpretation of your docking result
Binding strength: A best pose of −5.9 kcal/mol suggests weak binding for a kinase target; ATP-site inhibitors for JAK1 typically show ≤ −8 to −10 kcal/mol in similar docking setups.
Pose consistency: Multiple poses with RMSD ~2.0–3.3 Å indicate a cluster but not tight convergence. The presence of very large RMSDs (12–21 Å) suggests alternative, likely non-specific poses.
Ligand chemistry: Ascorbic acid is small, highly polar, and often deprotonated at physiological pH, which can lead to shallow or solvent-exposed binding and overestimated docking due to H-bond scoring without desolvation.
Immediate checks to validate the setup
Redock the co-crystal ligand:
Re-dock the native ligand from the same JAK1 structure and confirm you can reproduce its pose within ≤2.0 Å RMSD.
Use that as a positive control; include a known JAK1 inhibitor and a negative control (e.g., a non-binder).
Binding site definition:
Confirm the docking box is centered on the ATP binding site (hinge region: typically residues engaging H-bonds with adenine).
If you targeted an allosteric pocket, specify and validate with a reference ligand.
Protein preparation:
Protonation states: Ensure JAK1 catalytic residues and ligand protonation are set for pH ~7.4. Ascorbate often exists as monoanionic; test both neutral and anionic forms.
Missing atoms/waters: Retain conserved catalytic water(s) if known; removing all waters can distort H-bond networks in the hinge.
Tautomer/rotamers: Check key side chains (e.g., Lys, Glu/Asp) for reasonable orientations.
Docking parameters:
Increase search thoroughness (exhaustiveness/number of runs) to test convergence.
Cluster poses and report the top cluster size and mean RMSD to judge stability.
Strengthening the evidence
Rescore key poses:
Apply post-docking rescoring (e.g., MM-GBSA/implicit solvent) on the top 2–3 poses to factor desolvation.
If ΔG remains weak (around −5 to −6 kcal/mol), it’s unlikely to be a competitive binder.
Short molecular dynamics sanity check (1–5 ns):
Monitor H-bonds to hinge residues and ligand RMSD. Rapid drift indicates unstable binding.
Site mapping:
Run pocket analysis to verify whether ascorbate sits in a druggable cavity vs. a solvent-exposed surface.
Experimental follow-up (if computational support is weak)
Biochemical assay:
Test JAK1 kinase activity ± ascorbate at physiological pH and ionic strength.
Include ATP competition to see if any inhibition is ATP-site mediated.
Cell-based signaling readouts:
Measure STAT phosphorylation downstream of JAK1 with and without vitamin C.
Control for antioxidant/redox effects (ascorbate can alter metal/thiol states independent of binding).
Practical next steps
Confirm pocket targeting with a co-crystal redock and known inhibitor as a benchmark.
Repeat docking with corrected protonation states (ascorbate neutral vs monoanionic), include conserved waters, and higher sampling.
Cluster and rescore the top poses; proceed to quick MD if any pose shows plausible hinge H-bonds.
Decide go/no-go: If rescored ΔG remains weak and MD unstable, pivot to testing non-binding mechanisms (redox modulation) rather than direct JAK1 binding.
Plan assays to disentangle binding from antioxidant effects.
Would you like me to review the exact binding site you targeted (ATP vs allosteric) and the 5IXI residue environment? Also, do you have the top pose coordinates or interaction map to inspect the H-bond partners?
いい質問ですね!専門的な表現なので、分かりやすく整理してみますね。
文の意味の分解
「AUTODOCKでポケットのターゲティングを確認する」
AutoDock は分子ドッキングシミュレーションのソフトウェアです。
「ポケット」とはタンパク質の立体構造の中でリガンド(薬分子など)が結合する空間のこと。
つまり「AutoDockを使って、目的の結合部位(ポケット)にリガンドが正しく結合するかを確認する」という意味です。
「既知の阻害剤や共結晶化リガンドをリドックしてベンチマークとする」
「既知の阻害剤」=すでにそのタンパク質に結合することが知られている分子。
「共結晶化リガンド」=タンパク質と一緒に結晶化され、構造解析(X線結晶構造解析など)で結合状態が分かっているリガンド。
「リドック」=既知のリガンドを改めてドッキング計算にかけて、シミュレーション結果が実験構造と一致するかを確認すること。
「ベンチマークとする」=その結果を基準にして、AutoDockの設定や精度を評価すること。
全体の意味
つまりこの文章は、
AutoDockを使ってタンパク質の結合ポケットを狙ったドッキングを行い、既知の阻害剤や共結晶化リガンドを再度ドッキングして、実験データと一致するかを基準(ベンチマーク)として精度を確認する
ということです。
研究の流れイメージ
タンパク質の構造を用意する(PDBなど)。
既知のリガンドをAutoDockで再ドッキングする。
実験で得られている結合様式と比較する。
一致すれば「この条件で新しい化合物をドッキングしても信頼できる」と判断できる。
こうした「リドッキング+ベンチマーク」は、新規化合物の仮想スクリーニングに入る前の精度検証ステップなんです。
もしご希望なら、この「リドッキングの具体的な手順」や「評価指標(RMSDなど)」についても詳しく解説できますが、そちらも知りたいですか?
はい、その理解でほぼ正しいです 。もう少し丁寧に説明しますね。
PDB構造に低分子が結合している場合の扱い
PDBファイルには「共結晶化リガンド」や阻害剤が含まれていることが多い → これは実験的にタンパク質と一緒に結晶化され、結合状態が確認されている分子です。
ドッキングの準備では通常、この既知リガンドを一度外す(削除する) → AutoDockなどのドッキング計算では「空のポケット」に対して自分の候補リガンドを入れて結合を予測するためです。
その後、自分のLIGANDをドッキングする → 新しい化合物がそのポケットにどのように結合するかをシミュレーションします。
ただし重要なステップ
リドッキング(既知リガンドを再ドッキング)
既知リガンドを外して、もう一度AutoDockでドッキングしてみる。
実験構造とシミュレーション結果が近ければ(RMSDが2Å以下など)、その条件設定は信頼できる。
ベンチマークとして利用
リドッキングで精度を確認した後に、自分の新しいリガンドをドッキングする。
これにより「このポケットに正しくターゲティングできている」と安心して解析できる。
まとめ
はい、まず既知の低分子を外してから自分のリガンドを入れる流れです。
ただし、その前に「既知リガンドをリドッキングして精度検証」を行うのが重要です。
もしご希望なら、「リドッキングの精度評価に使う指標(RMSDの計算方法など)」についても具体的に解説できますが、そちらも知りたいですか?
いいところに目をつけましたね。「ベンチマーク」という言葉は、ドッキングや計算化学の文脈では少し専門的な意味で使われます。
ベンチマークの基本的な意味
一般的な意味 「基準」「ものさし」「比較対象」となるもの。性能や精度を測るための標準です。
ドッキングにおける意味
既知の阻害剤や共結晶化リガンドを使って、計算条件が正しく働いているかを確認すること。
実験で分かっている結合様式と、シミュレーションで得られた結合様式を比較する。
これが一致すれば「この設定で新しいリガンドを試しても信頼できる」と判断できる。
具体例
PDBに既知リガンドがある場合
そのリガンドを外して、AutoDockで再ドッキングする。
実験構造とシミュレーション結果を比較する(RMSDなどで評価)。
結果が良ければ
その条件を「ベンチマーク済み」として、新しいリガンドのドッキングに使う。
結果が悪ければ
グリッドの設定やパラメータを見直す必要がある。
まとめ
「ベンチマークする」とは、既知のリガンドを使ってドッキング条件の精度を検証し、その結果を基準にすることです。 つまり「新しいリガンドを試す前に、計算条件がちゃんと機能しているかを確認するためのテスト」ですね。
よければ、次に「ベンチマークでよく使われる評価指標(RMSDやスコアの比較)」についても解説しましょうか?
では「ベンチマークでよく使われる評価指標」について詳しく説明しますね。
ドッキング精度の評価指標
1. RMSD (Root Mean Square Deviation)
意味:実験で得られたリガンドの結合位置と、ドッキングで予測された位置のずれを数値化したもの。
計算方法:原子座標の差を二乗平均して平方根を取る。
目安:
RMSD ≤ 2 Å → 良好な再現性(ドッキング条件が信頼できる)。
RMSD > 2 Å → 結合様式の再現性が低い可能性。
2. スコア(ドッキングスコア/binding energy)
AutoDockでは「自由エネルギー推定値(binding free energy)」が出力されます。
値が より負(低い)ほど結合が強いと予測されます。
ただし絶対値よりも「相対比較」が重要。既知リガンドと新規リガンドを比べて、どちらがより安定に結合しそうかを判断します。
3. 結合ポーズの再現性
ドッキング計算では複数の「ポーズ(結合様式)」が出力されます。
既知リガンドの実験構造と似たポーズが上位に出てくるかどうかを確認します。
クラスタリング解析で「同じようなポーズが多数出ている」場合は信頼性が高いと考えられます。
4. 相互作用の比較
実験構造で確認されている水素結合や疎水性相互作用が、ドッキング結果でも再現されているかをチェック。
これにより「ポケットのターゲティングが正しくできているか」を確認できます。
まとめ
ベンチマーク=既知リガンドを使って条件の妥当性を確認すること
評価指標=RMSD、ドッキングスコア、ポーズの再現性、相互作用の一致
これらを満たせば「新しいリガンドを試す前に、計算条件が信頼できる」と判断できます。
次のステップとしては、「RMSDを実際に計算する方法」や「AutoDockで出力されるログの読み方」を解説すると実践に役立ちますが、そちらも知りたいですか?
では、RMSDの計算方法やAutoDockのログの読み方について解説しますね。
RMSDの計算方法
RMSD(Root Mean Square Deviation)は、実験構造とドッキング予測構造の「原子座標のずれ」を数値化したものです。
計算式
NN:比較する原子の数
did_i:各原子ペアの距離差
実際には、リガンドの重心を合わせてから原子ごとの位置を比較します。
実務での目安
RMSD ≤ 2 Å → 実験構造をよく再現している(良好なベンチマーク)。
RMSD 2–3 Å → まあまあ再現できている。
RMSD > 3 Å → 再現性が低い、条件の見直しが必要。
AutoDockのログの読み方
AutoDockを実行すると、結果ファイル(通常 .dlg や .log)に以下の情報が出力されます。
Binding Energy(結合自由エネルギー)
単位は kcal/mol。負の値が大きいほど安定結合を予測。
Cluster Analysis(クラスタリング解析)
似たポーズをまとめて表示。
同じクラスタに多くのポーズが集まっている場合、信頼性が高い。
Best Docking Pose(最良ポーズ)
最も低いエネルギーを持つポーズ。
実験構造と比較してRMSDを計算する対象になる。
実際の流れ
PDBから既知リガンドを取り出す。
AutoDockでリドッキングを行う。
出力ログから最良ポーズを確認。
実験構造と比較してRMSDを計算。
RMSDが基準値以内なら、その条件をベンチマークとして新規リガンドに適用。
まとめ
RMSDは「実験構造と予測構造のずれ」を数値化する指標。
AutoDockログでは結合エネルギーやクラスタリング結果を確認できる。
RMSD ≤ 2 Åなら「ベンチマーク成功」とみなして、新しいリガンド探索に進める。
次は「RMSDを実際に計算するためのツールやコマンド(PyMOLやAutoDockToolsでの操作方法)」についても解説しましょうか?
では、RMSDを実際に計算する方法と、AutoDockToolsやPyMOLでの具体的な操作手順を紹介しますね。
RMSD計算の実践方法
1. PyMOLを使う場合
手順
実験構造(PDBの共結晶化リガンド付き構造)を読み込む。
AutoDockで得られたドッキングポーズ(PDBQTや出力PDB)を読み込む。
リガンド部分を選択して重ね合わせる。
コマンド例:
コードalign docked_ligand, crystal_ligand
PyMOLが自動的にRMSDを計算して表示してくれる。
メリット:視覚的に重ね合わせを確認できる。相互作用の再現性も見やすい。
2. AutoDockTools (ADT) を使う場合
ADTには「Analyze → Docking → RMSD」機能があります。
手順
実験構造とドッキング結果を読み込む。
RMSD計算対象のリガンドを指定する。
ADTが自動的にRMSD値を出力。
メリット:AutoDockの出力ファイルと直接連携できる。
3. コマンドラインツールを使う場合
OpenBabelやRDKitなどの化学情報処理ライブラリでもRMSD計算が可能。
例:OpenBabel
コードobfit "SMARTSパターン" crystal_ligand docked_ligand研究で大量のリガンドを扱う場合に便利。
評価の目安
RMSD ≤ 2 Å → 良好な再現性
RMSD 2–3 Å → 許容範囲
RMSD > 3 Å → 条件の見直しが必要
まとめ
PyMOL → 視覚的に確認しながらRMSDを計算できる
AutoDockTools → AutoDockの結果と直接連携してRMSDを出せる
OpenBabel/RDKit → バッチ処理や自動化に便利
次は「RMSD以外に、ベンチマークでよく使われる追加評価(例えば相互作用解析やスコア比較)」についても解説しましょうか?
Autodock での結果差の解釈
「低分子(コファクター・結晶水・イオン等)を外す前のMACROでは結合が出たのに、外した後は出なくなった」という現象は珍しくありません。結合ポケットの物理化学環境や構造が低分子に依存しており、除去でポケットが崩れたり静電環境が変化した可能性が高いです。
よくある原因とチェックポイント
| 原因 | 典型的な症状 | 確認・対処 |
|---|---|---|
| コファクター依存性 | 補因子(金属、ヘム、NAD等)除去でスコア激減 | 可能なら補因子を残す、メタルパラメータの設定、金属結合想定のドッキング(必要に応じてcovalent/metal-aware法) |
| 結晶水の役割 | 媒介水除去で水素結合網が消失 | 構造水を選別して残す、仮想水を置く、グリッドに水相互作用を反映 |
| プロトネーション/電荷 | pH不整合で残基電荷が不適切 | pH条件でプロトネーションを再付与、ヒスチジンタウタマー確認、部分電荷再計算 |
| ポケットの閉塞 | 低分子除去後に側鎖が内向きで空間消失 | 柔軟残基設定(flexible residues)、短いMD/最小化でポケット再開、既知リガンドで再検証 |
| グリッド定義不適切 | 目的部位を外れている/サイズ不足 | 既知リガンド位置に合わせて中心・サイズ再設定、AutoGridでエネルギーマップ確認 |
| リガンド準備ミス | トートマー/プロトン化/部分電荷/回転結合の誤り | 立体化学・結合次数を再確認、トートマー/プロトン化状態を生理的条件に合わせる |
| スコア関数の限界 | 極性/メタル系で再現性低下 | Vina/AD4で比較、パラメータ調整、必要なら別ツールやMDで補完 |
Sources:
推奨する検証ステップ
準備の再確認
受容体:結晶水の選別(橋渡し水は残す)、金属・補因子の扱い、プロトネーションと部分電荷の付与をやり直す。
リガンド:トートマー・プロトン化状態・回転結合の定義・部分電荷を再チェック。
グリッドの再設計
既知リガンドやポケット中心に合わせて中心とサイズを見直し、AutoGridのマップを目視確認。
柔軟残基の導入
ポケット周辺のゲート残基(例:Tyr/Phe/His/Argなど)を柔軟に設定し、閉塞を回避。
対照実験
低分子「あり」と「なし」の両条件で同一ワークフローを実行し、スコア・ポーズの再現性を比較。既知インヒビターでポーズ検証。
手法の補完
極性が強い系・金属依存系では、スコア関数の相性問題が起こりやすい。Vina/AutoDock4の両方で試し、必要なら短時間MDやMM-GBSAで再スコアリング。
共有結合や金属配位が本質なら、該当プロトコルの利用を検討。
直感的な解釈
低分子を外すことで「ポケットの形・電荷分布・水素結合ネットワーク」が変わり、リガンドが本来の座位に収まりづらくなった可能性が高い。
これは構造の「静的なスナップショット」を前提とするドッキングの限界とも整合し、準備とパラメータの微調整で改善する余地があります。
必要なら、現在のPDB/グリッド設定/プロトネーション条件を教えてください。そこから最短で改善できる具体的な修正案を提案します。
77
[1-2] 分子ドッキング法を用いたリガンド結合構造予測と分子認識
金沢大学 理工研究域 数物科学系
齋藤 大明 saito@wriron1.s.kanazawa-u.ac.jp
概要
分子ドッキング法は計算コストも少なく,薬剤スクリーニングを効率化・迅速化させるための基盤技術と
して創薬の研究・開発に用いられている.本稿ではリガンド−タンパク質系を対象にしたドッキングシミュレ
ーションの基本的な計算手法・適用例について解説し,ドッキングシミュレーションの計算精度や適用限界
について言及し,今後の課題について考察する.
キーワード:リガンド,タンパク質,分子ドッキング法,分子動力学法
タンパク質は生体内において特定の基質やタンパク質を認識し,相互作用・分子会合することに
よりその機能を発現する.このようなタンパク質の分子認識メカニズムは結合サイト付近における
構造やダイナミクス(動的構造)と密接な関係があり,原子レベルでの構造変化と相互作用(結合
エネルギー)の詳細を明らかにすることが重要で
ある.
サイトを特定し,結合構造や分子親和性の詳細を明らかにする必要あり,これらを高速・高精度に
観測・予測・解析するための実験・理論的手法の開発が切望されている.
コンピュータを用いたリガンド−タンパク質の結合構造の予測に分子ドッキング法がある.一般
に分子ドッキング法は,リガンドと結合ポケット
の「形」の補償を満足する(すなわち「鍵と鍵穴」
の)構造を探索するアルゴリズムが用いられてい
る.計算コストも少なく,薬剤スクリーニングを
効率化・迅速化させるための基盤技術として創薬
の研究・開発に用いられている.分子ドッキング
は実験研究の結果のサポートや予測を与えるだけ
でなく,in silico による新規のタンパク質複合体の
モデリングにも有効である.しかしながら,計算
精度やレセプター構造のサンプル制限から適用限
界がある.加えてドッキング計算の結果は用いて
いる手法やアルゴリズム,計算パラメータの取り
方に大きく依存しており,有効活用のためには計
算プログラムの計算手法やアルゴリズムの理解が
必須である.
本稿ではリガンド−タンパク質系を対象にした
ドッキングシミュレーションの基本的な計算手
法・適用例について解説し,ドッキング計算の精
度や適用限界,今後の課題について検討する.
2. 方法
2.1 計算手順
分子ドッキングの計算プログラムはこれまで数
多く開発されており,計算プログラムは60以上,
リガンド−タンパク質の結合エネルギー評価のた
めのスコア関数は30以上開発されている[1].
各々のドッキングプログラムでは独自の計算手法
やアルゴリズムを用いて,リガンド−タンパク質の
結合エネルギーや結合構造の予測を行っているが,
計算手順の大枠は共通で,以下の手順に従う.
・Preparation
・Posing
・Scoring
・Ranking
始めにリガンド・タンパク質の分子座標を用意し
(Preparation),タンパク質の結合ポケット内でのリ
ガンド分子の配座探索を行う(Posing).その後
Posing によって作成したリガンド分子とタンパク
質との分子親和性(結合エネルギー)をスコア関
数を用いて評価を行い(Scoring),最後に,作成し
た各々のリガンド配座をスコア値順にソートして
最も possible なリガンド結合構造を決定する
(Ranking).以下では計算のメインとなるPosingと
Scoring の方法について解説する.
2.2 Posing:リガンド分子の配座探索
ドッキング法に用いられるリガンドの配座探索
アルゴリズムは,Multi-conformer, Stochastic,
Consensus docking の3つが主に知られている[2].
Multi-conformer と Stochastic docking は共にポケ
ットとリガンド分子の形状・相互作用の補償が良
い配座を探索する方法で,Stochastic dockingでは
リガンドの配座探索にgeneric algorithm (GA)やモ
ンテカルロ法を用いる.これらの手法はDOCK [3]
や AutoDock [4],GOLD [5]等の多数の計算プログ
78
The Molecular Simulation Society of Japan
ラムに用いられている.また,分子動力学(MD)
シミュレーションを行い,リガンドの結合分子ポ
ーズ作成を作成した後,分子ドッキング法で用い
られるスコア関数を用いて結合エネルギーを評価
する方法もある.Consensus ドッキング法は発生
させたリガンド分子配座の相互作用を2〜3つの
スコア関数を用いて評価する方法で,評価したリ
ガンドの結合分子ポーズの正当性を向上させる方
法である[2].
2.3 Scoring:スコア値評価
結合エネルギー評価のためのスコア関数は主に
Empirical-base, Force field-base, Knowledge-base の
3つに分類される[2].Empiricalスコア関数は次式
に示す様にリガンド−タンパク質間の結合エネル
ギーを5〜7つの項(水素結合や静電相互作用,
疎水性相互作用等)に分けて評価し,それら項目
の和によって結合エネルギーを定義する.
∆bind = ∑∆i(,)
ここで,rl, rpはそれぞれリガンド,タンパク質の
座標を表す.各々のエネルギー項fi(rl,rp)の結合エ
ネルギーΔGbindへの寄与は,経験的に決定される
スケーリング係数ΔGiによって決定される.各項
の関数定義やパラメータは Empirical スコア関数
の定義によって異なる.
Force field-base のスコア関数は次式に示すよう
にvan der Waals (vdW)相互作用とクーロン相互作
用の2項の和で表されており,一般的な分子動力
学法の分子間相互作用ポテンシャルと同じような
関数形を持つ.
�
�
∆ = ∑∑[
12
−
6
+332.0
]
ここでA, Bは各原子タイプに適用されるvdWパ
ラメータ,q は原子電荷のパラメータを表す.
DOCK では Amber 力場で用いられる vdW・原子
電荷のパラメータを適用してリガンド−タンパク
質の結合エネルギーを評価する.関数形は各計算
プログラムで一様ではなく,例えば AutoDock で
はさらに水素結合相互作用を考慮した項が加えら
れる(Amber untied-atom 力場と同型).
Knowledge-based のスコア関数は,実験で解か
れている多数のリガンド−タンパク質複合体の結
晶構造データから各原子−原子の原子間距離に対
する分布関数(ヒストグラム)を数値的に作成し,
これを用いてリガンド−タンパク質間の結合親和
性を数値的に決定する.これは DrugScore[6]や
PMF[7] 等のドッキングプログラムで採用されて
いる.
2.4 溶媒和・エントロピー効果
前節に示した Empirical-base や Force field-base
のスコア関数はリガンド−タンパク質間の分子間
相互作用を評価するもので,リガンド結合による
溶媒和やエントロピー変化は考慮されていない.
幾つかの計算プログラムでは,これらは別の方法
で評価し,これをスコア値に加えることで新たに
結合エネルギーを定義している.例えばAutoDock
ではこれらのエネルギー項を簡単な関数形とパラ
メータで表し,これら項目を加えた関数を新たに
リガンド−タンパク質の結合自由エネルギーとし
て計算する[4].DOCKではオプションとして,前
出のスコア関数で得られたスコア値に加えて,作
成したリガンド−タンパク質の結合ポーズの分子
座標からPoisson Boltzmann surface area (PBSA)[8]
やgeneralized Born surface area(GBSA)法[9]を用い,
リガンド・タンパク質の溶媒和による結合自由エ
ネルギーの寄与を計算することができる.これら
溶媒和による効果を加えることにより高精度な分
子スクリーニングが可能となる[10].
ここで紹介したスコア値と実験で観測される結
合エネルギーとの比較は注意が必要である.ドッ
キングシミュレーションでは系は explicit な溶媒
分子を含まず,リガンドと標的タンパク質の構造
のみで相互作用を評価するため,本質的に生体内
のリガンド−タンパク質と対応する相互作用とは
ならない.そのため,幾つかのスコア関数では実
験結果を再現するためのスケーリング係数が導入
されている.ところが,DOCK等で使われるスコ
ア関数では各項の値を実験値に近づけるためのス
ケーリングパラメータを含まないことから,
Empirical base や一部のスケーリングパラメータ
を含んだForce field base の結果と大きく異なる.
実際,PBSA法やGBSA法を用いた計算でも実際
の実験値の値に比べて非常に大きな値を示すこと
が知られている[10].あくまでもスコア値は作成
した分子配座から最もpossible なポーズを決定す
ることや,同じスコア関数を用いた化合物のスク
リーニングに用いられることに留意したい.
分子シミュレーション研究会会誌“アンサンブル”Vol. 17, No. 2, April 2015 (通巻70号)
79
(a)
(b)
図1: (a) L-Arabinose 結合プロテインのスナップ
ショット構造(PDB ID: 1ABE), (b) L-Arabinose
3 適用例
本節では実際の適用計算の例として,自作のド
ッキングプログラムを用いた具体的な計算例につ
いて紹介する.計算に用いるアルゴリズムとスコ
ア関数はDOCKと基本的に同じである.計算は2
節に示した計算手順(2.1)に従って行う.本稿で
はテストモデルとして L-Arabinose 結合プロテイ
ン(PDB ID: 1ABE)を用いた.1ABEはリガンド分
子が結合した状態のリガンド−タンパク質複合体
の結晶構造であり,この複合体構造からリガンド
分子を取り出し,これをタンパク質の結合サイト
周辺にドッキングさせる計算を行う(いわゆる
Re-docking シミュレーションを実行する).
3.1 リガンド・レセプター座標の準備
はじめに PDB のリガンドとタンパク質座標に
は水素の原子座標がないので,これらを chimera
[11]等のモデリングツールを用いて添加する(図1
参照).その後,リガンド−タンパク質間のスコア
値評価のための各原子の原子タイプと部分電荷パ
ラメータのassign を行う.こちらもchimera を用
いて行うことができる.各原子タイプのvdWパラ
メータはAmber99 力場[12]が適用され,部分電荷
の決定にはsemi-empirical のMO計算(AM1-bcc)が
適用される.
3.2 結合ポケットの決定
標的タンパク質の結合ポケットサイト同定のた
めに,まず始めにタンパク質表面座標の生成を行
う(図2(a)参照).これら表面座標の作成もchimera
(a)
(b)
図2: (a) L-Arabinose 結合プロテインの表面構造,
(b) 結合ポケット周辺のsphereクラスタ分布
を用いて行った.
その後に,タンパク質表面にその表面座標と接
触するsphere(球)を多数発生させる.タンパク
質表面のくぼみがある領域(ポケット領域)では
発生させたsphere同士で重なりが生じ,sphereク
ラスタが造られる.これらsphereクラスタで造ら
れる空間がタンパク質のポケット形状と同型(つ
まり「鍵穴」の構造となる)となることから,こ
の sphere クラスタの座標がリガンド分子(「鍵」
構造に対応)ドッキングのターゲット座標となる
[13].
この様なsphereクラスタはタンパク質表面上に
幾つか存在し,それら全てが結合ポケットの候補
となる.通常はこれらsphereクラスタの内で最も
大きなクラスタを作るものが最もpossible な結合
ポケットとなる(もちろんそうでない場合もある).
本モデルではすでに「正解」のリガンドの分子座
標(複合体の結晶構造におけるリガンドの分子座
標)が分かっているので,このリガンド座標周辺
(< 10 Å)のsphereクラスタの座標をドッキング
のターゲット座標とした.図2(b)に結合ポケット
周辺で選別したsphereクラスタの様子を示す.図
2(a)との比較からタンパク質の中央部分に大きな
くぼみ領域が存在し,この領域にsphereクラスタ
が生成されている様子が示されている.
3.3 グリッドエネルギー計算
続いてドッキングサイト(sphereクラスタ)を
取り囲むBox領域を作成し,この領域内に細かい
目(x, y, z 共に 0.3Å程度)のグリッド点を作成す
80
The Molecular Simulation Society of Japan
図3: 結合ポケット周辺のグリッド領域(白線)
る.通常のドッキングシミュレーションではタン
パク質の原子座標は固定されるので,タンパク質
の原子からの相互作用寄与をこれらグリッド点に
代表させることによって,リガンド−タンパク質間
の相互作用計算を高速に行うことが可能となる
[14].Box の大きさはx, y, z 共に sphere クラスタか
ら5Å程度離して作成する(図3参照).
3.4 ドッキング&エネルギー最小化
作成したsphereクラスタ座標へリガンド分子を
配置(ドッキング)させる.リガンド分子の配置
にはiso-morphous subgraph matching 法 [3]を用い
る.これにより,sphere クラスタ内の形状とリガ
ンド分子の形状の補償が良い分子配座を作成する
ことが出来る.この1ABEモデルでは495の初期
分子配座が作成された.
これらの初期のリガンド配座は単にポケットと
の形状補償が良いだけで,相互作用的には最適な
分子配座となっていない.そこでリガンド分子の
並進・回転,そしてリガンド分子内の2面角を変
化させることによりポケット内の分子配座の最適
化を続いて行う.最適化にはDownhill Simplex法
[15]を用いた.Simplex に用いる変数(vertex)は分子
の並進・回転・2面角とし,これらの値を変化さ
せ,逐次,スコア値を計算し,スコア値の変化が
一定の値に収束するまで繰り返す.
3.5 ランキング&解析
分子配座の最適化を全ての作成した初期リガン
ド配座に対して行う.最適化されたリガンド配座
分子のスコア値を比較し,スコア値が良い順(エ
ネルギー値が低い順)にソートすることにより,
ドッキングよる結合構造が最終的に決定される.
この様にして決定されたリガンドの結合構造の
正当性の評価のために,最適化されたリガンド配
図4: RMSD値に対するスコア値の分布
図5: 基質の結晶構造とドッキング構造(シアン)
座の分子座標と複合体の結晶から得られる「正解」
のリガンドの分子座標との根平均自乗変位(Root
Mean Squared Displacement: RMSD)を計算した.図
4 に最適化された495個のリガンド分子のRMSD
に対するスコア値の様子を示す.この図が示す様
に,RMSDの値が低い分子配座はスコア値も低い
傾向が明確に示された.さらにスコア値が最も低
い分子配座は RMSD 値も最も低くなる結果が示
された.図5に「正解」のリガンド配座とドッキ
ングによって予測された結合配座の比較を示す.
2つのリガンド構造は殆ど重なり,RMSDの値も
0.19Å であったことから,ほぼ「正解」のリガン
ド構造を再現する結果が得られ,用いた初期座標
やスコア関数,最適化法が適切であることが示さ
れた.
3.6 リガンド−タンパク質複合体setへの適用
前節までの手法を 114 個のリガンド−タンパク
質複合体のtest set [16]へ適用し,ドッキングの成
功率についての評価を行った.ここで,ベストス
コアを示すリガンドの分子座標と「正解」のリガ
ンドの分子座標とのRMSDが2Å以内でれば「正
解」と定義した.計算の結果,114個のうち90個
が「正解」の構造と判断され,およそ80%の確率
分子シミュレーション研究会会誌“アンサンブル”Vol. 17, No. 2, April 2015 (通巻70号)
81
で「正解」の構造を予測できる結果が示された.
4 結果考察と今後の課題
本節では前節までの結果の考察と,実際の分子
スクリーニングを行う際に考慮すべき点について
考察する.
4.1 Re-docking 計算の結果考察
ほとんどの分子ドッキングプログラムはタンパ
ク質の分子認識における基本概念である「鍵と鍵
穴」をベースに,計算アルゴリズムが設計されて
おり,「鍵」であるリガンド分子の形状と,「鍵穴」
であるレセプターのポケット形状の補償が良いリ
ガンド配座を見つけ,そのポケットサイトへのド
ッキングとリガンド分子の配座の最適化により,
高精度なリガンド−タンパク質複合体の
Re-docking シミュレーションを実現している.
非常に単純な計算アルゴリズムとスコア関数を
用いたにもかかわらず,高精度の成功率を示した
のには幾つかの理由があると考える.まず,今回
のtest set ではあらかじめリガンド−タンパク質の
結合構造が分かっている系であることが挙げられ
る.計算手順の記述にあるように,正解構造が分
かっている系では「正解」構造周辺にドッキング
のターゲット座標(sphere クラスタ)が作成される
ので,これはすでに知っている「正解」の構造付
近にドッキングシミュレーションをしていること
に対応する.
またドッキングに用いているレセプターの分子
座標をリガンド−タンパク質複合体の結晶構造か
ら取り出して用いていることも要因の一つであろ
う.一般的にタンパク質は結合するリガンド分子
の構造にマッチするように,ポケットの形状を変
化させている.より専門的な表現で言えば
“Induced fit”,もしくはリガンド結合によるポケッ
ト構造の“Population shift”が起きていることにな
る.リガンド分子の形状にマッチする形のポケッ
トへのドッキングシミュレーションは形が合う鍵
穴へ鍵を指すことに近いだろう.
4.2 Ensemble-based docking
このことから,たった1つのレセプターの分子
座標を用いて分子スクリーニングを行う場合,あ
る特定の(そのポケット形状とたまたま構造補償
が良い)化合物に対しては良いスコア値を示すか
もしないが,本来もっと良い活性を示すはずの化
合物に対して(たまたま構造補償が悪いために)
悪いスコア値を示す可能性がある.そのため,様々
なポケット形状をもつタンパク質の分子構造を多
数用意し,それらのレセプター構造に対して,ド
ッキングシミュレーションを行う Ensemble-based
ドッキングはより正当性の高いスクリーニング法
と言える[17].しかしながら,この手法は実験で
多数のレセプター構造が解かれているターゲット
タンパク質に限定されることから,サンプル数が
少ないタンパク質の場合は適用ができない問題が
ある.
また近年の実験・理論的研究によると,生体中
のタンパク質の結合ポケットはいくつかの安定形
状の構造を持ち,動的に構造遷移を繰り返してい
ることが知られている.基質はこれら安定構造の
うち,形状補償が良い結合ポケットと会合し結合
構造を安定化(Population shift)させていることが
明らかとなってきた[18].すなわち,より現実の
分子認識機構に即した分子ドッキングを行うには,
分子動力学(MD)シミュレーション等により作成
された「結合ポケットの形状変化を含めたアンサ
ンブル構造に対しての分子ドッキング」を行うべ
きであり,これを実現する計算手法の開発と実地
研究が今後の重要課題であると考える[18].
謝辞
本稿と関連した研究は文部科学省科学研究補助
金「新学術領域研究:天然物ケミカルバイオロジ
ー」[19]からのサポートにより行われた.本研究
の計算は自然科学研究機構 計算科学研究センタ
ーの利用により行われた.
参考文献
[1] Sousa, S. F., Fernandes, P. A., & Ramos, M. J.,
Proteins-Structure Function and Bioinformatics,
65(1), 15–26 (2006).
[2] Waszkowycz, B., Clark, D. E., & Gancia, E.,
Computational Molecular Science, 1(2), 229–259
(2011).
[3] P. Therese Lang; Scott R. Brozell; Sudipto
Mukherjee; Eric F. Pettersen; Elaine C. Meng;
Veena Thomas; Robert C. Rizzo; David A. Case;
Thomas L., RNA, 15:1219–1230, (2009).
[4] Garrett M. Morris; Ruth Huey; William Lindstrom;
Michel F. Sanner; Richard K. Belew; David S.
Goodsell; Arthur J. Olson, J. Comput. Chem. 30:
2785–2791, (2009).
[5] Marcel L. Verdonk; Jason C. Cole; Michael J.
82
The Molecular Simulation Society of Japan
Hartshorn; Christopher W. Murray; Richard D.
Taylor, PROTEINS: Structure, Function, and
Genetics 52:609–623, (2003).
[6] Holger Gohlke, Manfred Hendlich and Gerhard
Klebe, J. Mol. Biol. 295, 337-356 (2000).
[7] Ingo Muegge and Yvonne C. Martin, J. Med.
Chem., 42, 791–804 (1999).
[8] David C. Thompson, Christine Humblet and Diane
Joseph-McCarthy, J. Chem. Inf. Model., 48, 1081
1091 (2008).
[9] Hawkins, G.D., C.J. Cramer, and D.G. Truhlar,
Chem. Phys. Lett., 246, 122-129, (1995).
[10] Junmei Wang, Paul Morin, Wei Wang, and Peter
A. Kollman, J. Am. Chem. Soc., 123, 5221-5230
(2001).
[11] Pettersen EF, Goddard TD, Huang CC, Couch GS,
Greenblatt DM, Meng EC, Ferrin TE. J Comput
Chem. 25,1605-12 (2004).
[12] K. Lindorff-Larsen, S. Piana, K. Palmo, P.
Maragakis, J.L. Klepeis, R.O. Dror and D.E. Shaw,
Proteins, 78,1950 (2010).
[13] Shoichet, B. K., Kuntz, I. D., & Bodian, D. L., J.
Comp. Chem., 13, 380-397 (1992).
[14] Meng, E. C., Shoichet, B. K., & Kuntz, I. D., J.
Comp. Chem., 13, 505-524 (1992).
[15] J. A. Nelder and R. Mead, The Computer Journal
7, 308-313 (1965).
[16]http://dock.compbio.ucsf.edu/Test_Sets/index.htm
[17] Maxim Totrov and Ruben Abagyan, Current
Opinion in Structural Biology, 18, 178-184
(2008).
[18] Ferran Feixas, Steffen Lindert, William Sinko a,b,
J. Andrew McCammon, Biophysical Chemistry
186, 31-45, (2014).
[19] M. Ueda, Chem. Lett., 41, 658-666 (2012).
著者紹介
音楽鑑賞.
齋藤 大明 氏(博士(理学)):
〔経歴〕2003年金沢大学大学院
自然科学研究科博士後期課修了,
2005 年産業技術総合研究所 計
算科学研究部門 契約職員.2008
年から現所属.〔専門〕分子シミ
ュレーション, 物理化学〔趣味
1pwcはβ-lactamaseのSer側鎖とpenicillin Gとが共有結合した複合体です。本記事ではAutoDock4 (ad) のcovalent dockingで、β-lactamaseのapo体から1pwcを再現します。
adでcovalent dockingを行うにはMGLToolsに含まれていないpythonスクリプトを使用する必要があります。そこでCovalent Docking - AutoDockからadCovalentDockResidue_v1.2.tar.gzをダウンロードし、コマンドプロンプトで解凍します。本記事は、解凍後のフォルダのREADME.txtに沿ってcovalent dockingします。
tar -xvf adCovalentDockResidue_v1.2.tar.gz
1. ファイルの準備
ドッキングに必要なligandとreceptorとを準備します。ligandのpenicillin GはPubChemから3次元構造をダウンロードしてきます。またreceptorのβ-lactamaseはPDBからダウンロードしてきます。
1-1. receptorの準備
PDBからβ-lactamaseのapo体である3PTEをダウンロードします。PyMOL等で3pte.pdbから結晶水を消去し、receptor.pdbとして保存します。
1-2. ligandの準備
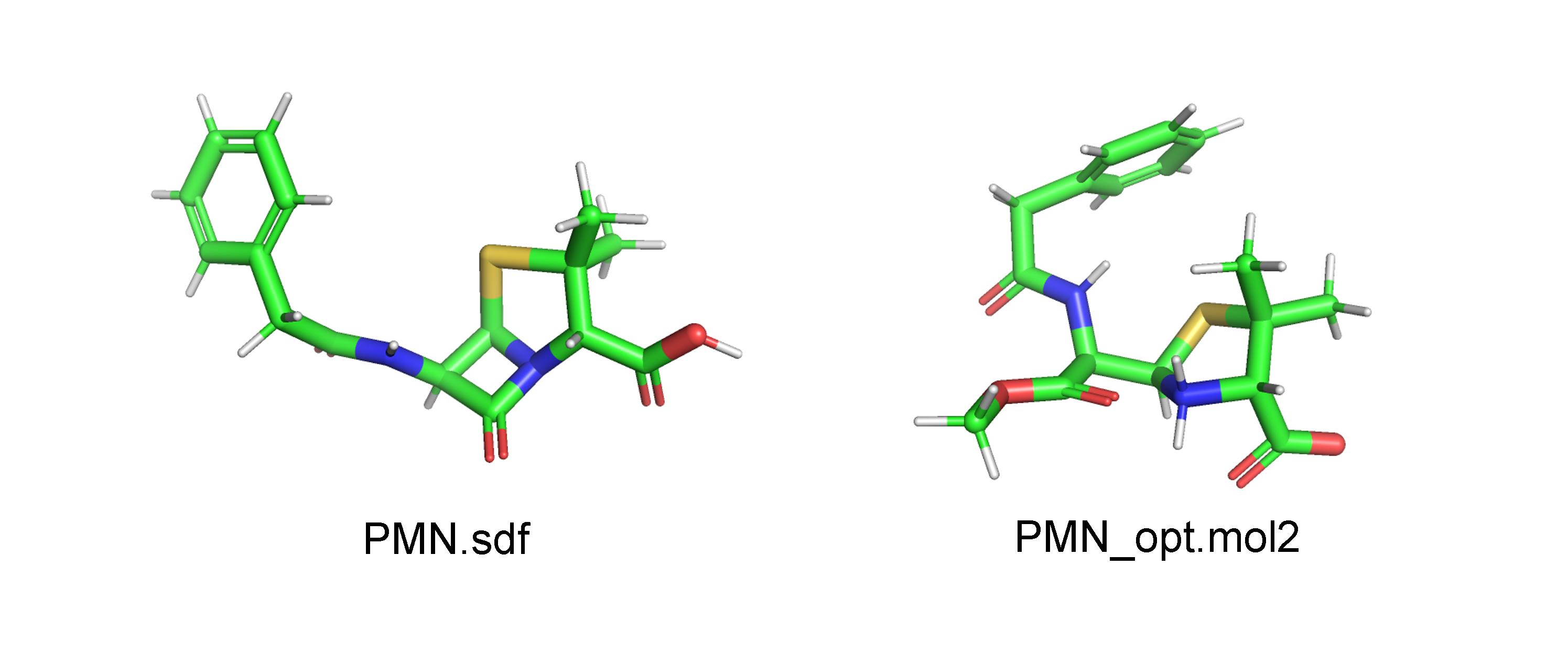
結合する残基がSerである場合、構造にMeOHを付加したligandを作成します。初めにPubChemから3次元構造(sdf形式)をダウンロードし、ファイル名をPNM.sdfに変更します。続いてPyMOL等でMeOHが付加した開環体をモデリングし、PNM_MeOH.mol2(mol2形式)として保存します。ダウンロードしてきた3次元構造ではプロトン化状態が中性付近のものでないため、その修正もここでしておきます。最後にPNM_MeOH.mol2をChem3D等でエネルギー最小化し、PNM_MeOH_opt.mol2として保存します(図1)。
2. prepareCovalent.py
先ほどダウンロードしたpythonスクリプト(prepareCovalent.py)で、receptorのSer側鎖とligandに付加したMeOHと重ね合わせます。
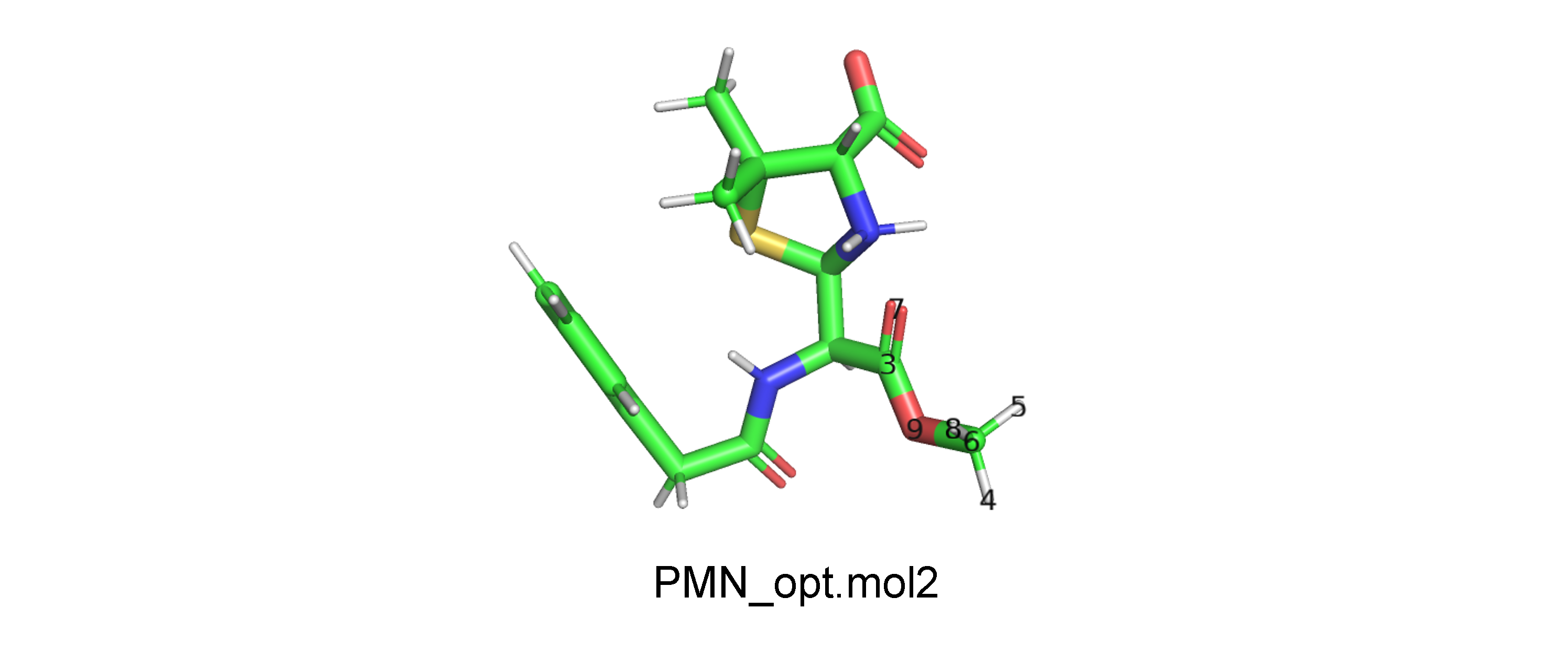
まず、PNM_MeOH_opt.mol2においてMeOHのC, Oが何番目の原子であるのかを確認します(図2)。Cが6番目、Oが9番目であることから、--ligindicesを6,9とします。
続いて、receptor.pdbにおいてどのSer残基がligandと共有結合するかを確認します。先行研究からreceptor.pdbはChainA 62番目のSer側鎖でpenicillin Gと結合していることから、--residueをA:SER62とします。
mgltoolsをインストールした仮想環境で以下を実行するとligcovalent.pdbが出力されます。
pythonsh /path/to/adCovalentDockResidue/adcovalent/prepareCovalent.py \
--ligand PMN_MeOH_opt.mol2 \
--ligindices 6,9 \
--receptor receptor.pdb \
--residue A:SER62 \
--outputfile ligcovalent.pdb
receptor.pdbとligcovalent.pdbとを描画すると、receptorとligandとが衝突していることがわかりますが、ここでは問題ありません(図3)。
図3. receptor.pdbとligcovalent.pdbとの衝突
3. PDBQTへの変換
receptor.pdbとligcovalent.pdbとをadで取り扱うためPDBQT形式に変換します。mgltoolsをインストールした仮想環境で以下を実行すると、それぞれをpdbqt形式に変換したファイルが出力されます。
# receptor.pdbの変換 (receptor.pdbqtが出力される)
pythonsh /path/to/envs/mgltools/MGLToolsPckgs/AutoDockTools/Utilities24/prepare_receptor4.py \
-r receptor.pdb \
-o receptor.pdbqt \
-U nphs_lps_waters \
-v
# ligcovalent.pdbの変換 (ligcovalent.pdbqtが出力される)
pythonsh /path/to/envs/mgltools/MGLToolsPckgs/AutoDockTools/Utilities24/prepare_ligand4.py \
-l ligcovalent.pdb \
-o ligcovalent.pdbqt \
-v
4. flexible/rigid PDBQTの生成
adのCovalent Dockingではligandをflexible residueとして扱います。そのためにreceptor.pdbqtとligcovalent.pdbqtとを、それぞれflexible partとrigid partとに分けます。
# receptor.pdbqtの変換 (receptor_rigid.pdbqt、receptor_flex.pdbqtが出力される)
pythonsh /path/to/envs/mgltools/MGLToolsPckgs/AutoDockTools/Utilities24/prepare_flexreceptor4.py \
-r receptor.pdbqt \
-s receptor:A:SER62
# ligcovalent.pdbqtの変換 (ligcovalent_rigid.pdbqt、ligcovalent_flex.pdbqtが出力される)
pythonsh /path/to/envs/mgltools/MGLToolsPckgs/AutoDockTools/Utilities24/prepare_flexreceptor4.py \
-r ligcovalent.pdbqt \
-s ligcovalent:A:SER62
Covalent dockingにはreceptor.pdbqtのrigid partとligcovalent.pdbqtのflexible partとを使用します(図4)。
図4. AutoDock4のCovalent dockingで使用するファイル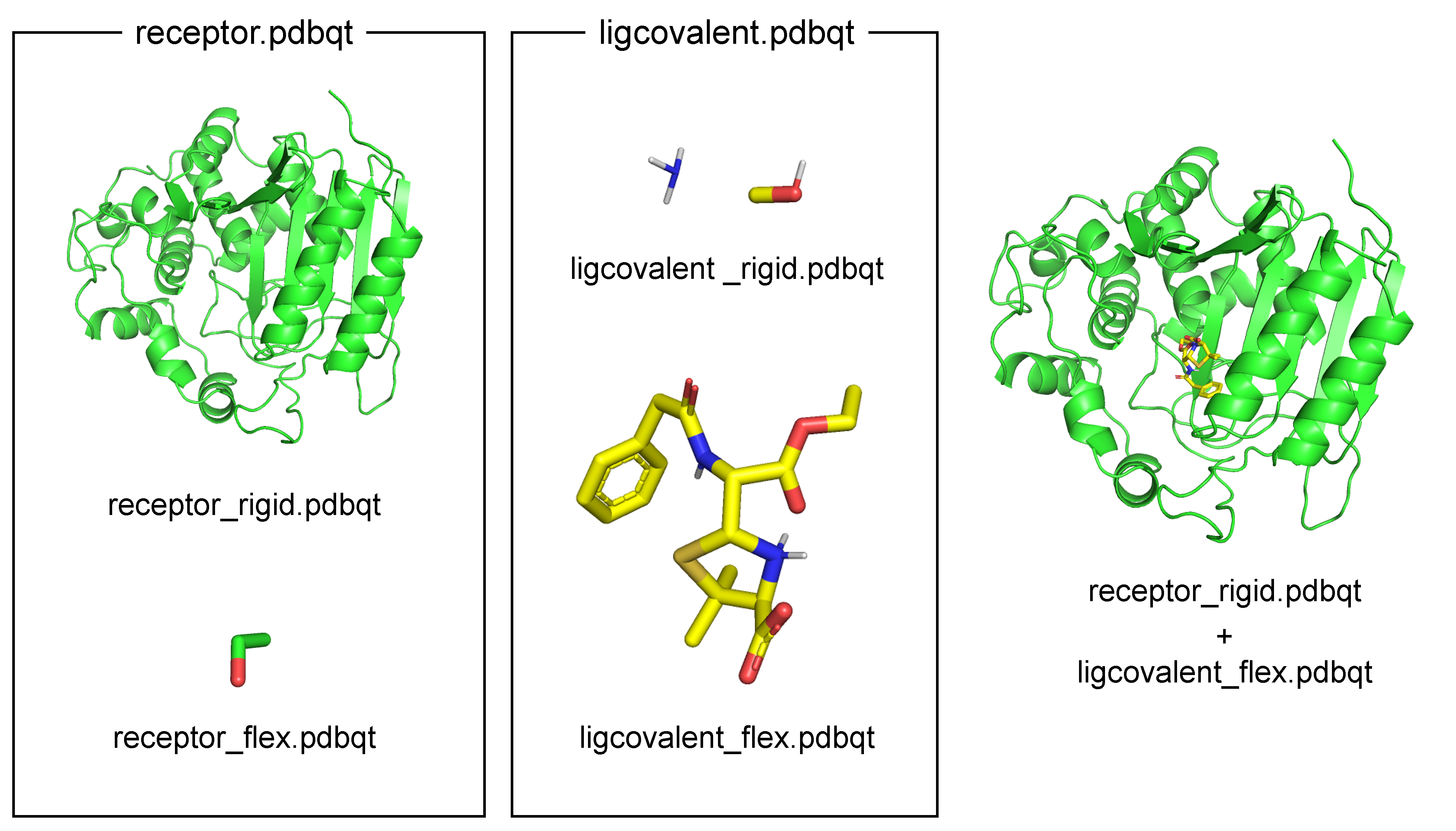
5. パラメータファイルの生成
ドッキング条件を指定するパラメータファイルを出力します。以下を実行すると、receptor.gpfとligcovalent_receptor.dpfが出力されます。
# .gpf (AutoGrid用のパラメーターファイル) の生成
pythonsh /path/to/envs/mgltools/MGLToolsPckgs/AutoDockTools/Utilities24/prepare_gpf4.py \
-r receptor_rigid.pdbqt\
-x ligcovalent_flex.pdbqt\
-l ligcovalent_flex.pdbqt\
-y -I 20\
-o receptor.gpf
# .dpf (AutoDock用のパラメーターファイル) の生成
pythonsh /path/to/envs/mgltools/MGLToolsPckgs/AutoDockTools/Utilities24/prepare_dpf4.py \
-r receptor_rigid.pdbqt\
-x ligcovalent_flex.pdbqt\
-l ligcovalent_flex.pdbqt\
-o ligcovalent_receptor.dpf\
-p move='empty'
# 空のファイルを作成しておく。
touch empty
生成されたligcovalent_receptor.dpfをメモ帳等で開き、unbound_model boundをunbound_energy 0.0に書き換えます。さらにga_runの値を10から100に書き換え、出力されるドッキングポーズを100個にします。
6. ドッキング
最後にドッキングします。autogrid4とautodock4とをインストールした仮想環境で以下を実行し正常に終了すると、ドッキングモデルが記載されたligcovalent_receptor.dlgが出力されます。
autogrid4 -p receptor.gpf -l receptor.glg
autodock4 -p ligcovalent_receptor.dpf -l ligcovalent_receptor.dlg
結果はadtから確認します。mgltoolsをインストールした仮想環境でコマンドプロンプトにadtと入力し実行すると、AutoDockToolsの画面が現れます。
- 画面右下の”Remind Me Later”が赤くなり次第、クリックする
Analyze → Docking → Open...によりligcovalent_receptor.dlgを開き、ドッキングポーズを表示するAnalyze → Macromolecule → Open...によりreceptor_rigid.pdbqtを開き、receptorを表示するAnalyze → Conformations → Play, ranked by energy...によりドッキングポーズをエネルギーが低い順にソートする- 一つずつドッキングポーズを確認し、確からしいポーズを選択する
右から2番目のボタン → Write Complexから表示しているポーズを保存する(図5)。
7. 答え合わせ
保存したドッキングポーズとX線結晶構造とを比較します。それらをPyMOLのalign機能で重ね合わせて答え合わせします。今回のドッキングシミュレーションでは出力した100ポーズの内、rank91とrank100とがX線結晶構造に近いということがわかりました。しかしrank91ではエステル結合の向きが、rank100ではカルボン酸の位置が1pwcと異なっています。また今回のように、設定条件にも依りますが、正しいポーズのランクが必ずしも良いとは限りません。
図6. rank91、rank100、X線結晶構造の重ね合わせ(灰色:1pwc、緑色:rank91、黄色:rank100)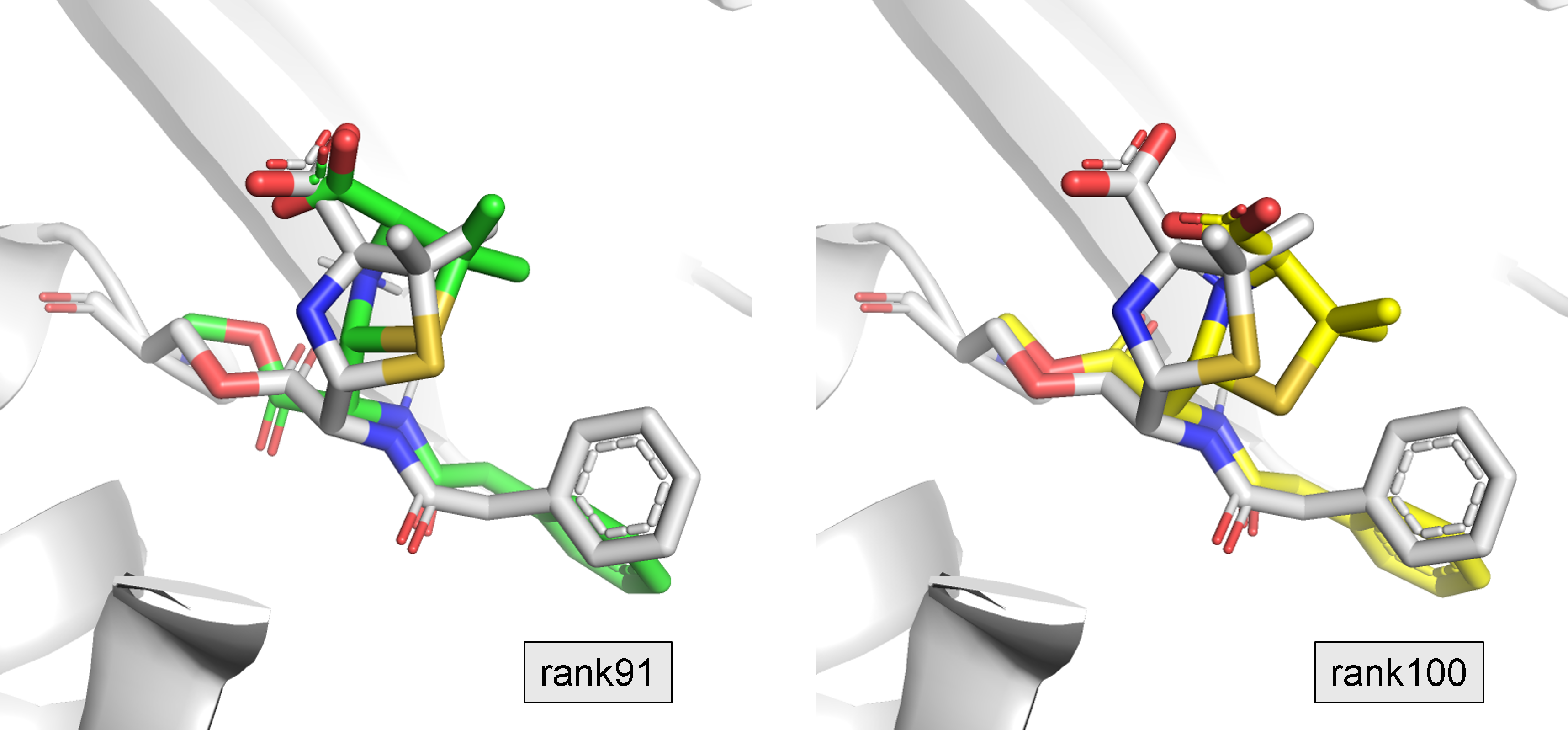
いい視点ですね!ただ、ここは少し整理が必要です。
RMSD と自由エネルギーの関係
RMSD (Root Mean Square Deviation) → ドッキング結果のポーズが「基準ポーズ」からどれくらいずれているかを示す指標。1.5~2 Å程度なら「ほぼ同じ位置に収まっている」と解釈できます。
自由エネルギー(binding affinity) → そのポーズの結合安定性をスコアリング関数で評価した値。もし複数ポーズでほぼ同じ値なら、結合の強さは大きく変わらないと考えられます。
⚖️ アロステリック効果との関係
アロステリック効果とは、リガンドが「本来の活性部位以外」に結合してタンパク質の構造や機能を変える現象です。
RMSD が 1.5~2 Å程度で自由エネルギーが同じ → これは「同じ結合部位にほぼ同じ姿勢で収まっている」ことを示すに過ぎません。
したがって、この情報だけから 「アロステリック効果はない」と断定することはできません。アロステリック効果の有無は、結合部位の場所(活性部位か別部位か)、タンパク質の構造変化、機能的影響などを総合的に見ないと判断できません。
まとめ
RMSD が小さく、自由エネルギーが同じ → 「同じ部位に似たポーズで結合している」と解釈できる。
しかし アロステリック効果の有無は RMSD と自由エネルギーだけでは判断できない。結合部位の位置やタンパク質の構造変化を確認する必要があります。
もし「アロステリック結合かどうか」を確かめたいなら、結合部位の座標を比較する、あるいは 分子動力学シミュレーションでタンパク質の構造変化を追うのが有効です。
ご希望なら「アロステリック結合を見分けるための解析手法」を整理してみましょうか?
では「アロステリック結合を見分けるための解析手法」を整理しますね。
アロステリック結合を見分けるための主な解析アプローチ
1. 結合部位の位置確認
ドッキング結果をタンパク質構造と重ね合わせ、リガンドが 既知の活性部位か、それ以外の部位(アロステリックサイト)に結合しているかを確認。
例: PDBデータベースや文献で報告されている活性部位座標と比較。
2. 複数ポーズの比較
RMSD が小さい場合は「同じ部位に似た姿勢で結合」している可能性が高い。
RMSD が大きく、結合部位が異なる場合は「別の部位=アロステリックサイト」の可能性。
3. 分子動力学シミュレーション (MD)
ドッキングだけではタンパク質の柔軟性を十分に反映できない。
MDシミュレーションでリガンド結合後のタンパク質構造変化を追跡し、活性部位の構造やダイナミクスが変化するかを確認。
4. 自由エネルギー計算
MM-PBSA や FEP などの手法で結合自由エネルギーをより精密に評価。
アロステリック結合の場合、活性部位のリガンド結合エネルギーやダイナミクスに影響を与えることがある。
5. 機能的アッセイとの統合
計算だけでは「アロステリック効果」を断定できない。
実験的に、リガンドが活性部位の基質結合や酵素活性に影響するかを確認する必要がある。
まとめ
RMSD と自由エネルギーだけではアロステリック効果は判断できない。
結合部位の位置、MDシミュレーションによる構造変化、自由エネルギー計算、そして実験的検証を組み合わせることで初めて「アロステリック結合かどうか」を見極められる。
ご希望なら、次に「実際に AutoDock Vina の結果からアロステリック結合を疑うときのチェックリスト」を作ってみましょうか?
AutoDock Vina 結果からアロステリック結合を疑うためのチェックリスト
クイックチェック(最初に見るポイント)
結合部位: 既知の活性部位か、それ以外のポケットかを可視化で確認する(Pocketビュー、既知リガンドとの重ね合わせ)。
ポーズ一貫性: 上位ポーズ間で位置が安定しているか(重心の位置、主要相互作用の再現性)。
相互作用プロファイル: 活性部位の必須残基と直接結合していないのに、遠隔残基と特徴的な相互作用があるか。
構造的チェック
距離と位置: 活性部位リガンド(基質や阻害剤)と新規リガンドの距離が十分離れているか(別ポケットに収まる)。
ネットワーク変化: 水素結合ネットワークや塩橋の再編成が示唆される相互作用(例:ヘリックス間のブリッジ、ループの固定化)。
保存性: 進化的に保存された活性残基ではなく、周辺の調節残基に結合しているか。
コンフォメーション依存性: オープン/クローズドなど、異なるタンパク質状態で結合部位が出現・消失するか(複数構造でドッキング比較)。
エネルギー・ダイナミクス評価
親和性の一貫性: 活性部位ポーズとアロステリック候補ポーズで親和性が近い場合、機能影響の可能性は残るため除外しない。
柔軟性の影響: MDで活性部位の距離、角度、ルート(ゲート開閉)の指標が変わるか(例:活性残基間距離の平均・分布の変化)。
結合安定性: MD中のリガンド RMSD/RMSF が低いか、主要相互作用が維持されるか。
コミュニケーション解析: ダイナミクスの相関(動的クロスコリレーション)、パス解析で結合部位から活性部位への情報伝達経路が強化/抑制されるか。
実験的裏付け(計算だけで断定しない)
活性アッセイ: 基質結合や触媒活性が濃度依存で変化し、競合(Ki, IC50の基質濃度依存性)パターンが競合的でないか。
結合同時性: 活性部位リガンドと同時結合が可能か(二者共存で活性変化が起きるならアロステリックの示唆)。
変異体検証: 予測したアロステリック残基の変異で効果が消失・反転するか。
構造法: HDX-MS、NMR、Cryo-EM/X線で遠隔のコンフォメーション変化が観測されるか。
よくある落とし穴
スコア過信: Vinaのスコアは近接相互作用中心で、長距離の構造変化は反映されにくい。
固定構造バイアス: 単一静止構造にドッキングすると、可動ループやゲートの影響を見逃す。
水分子無視: メディエーター水の除去で相互作用ネットワークを誤解する。
ポケット誤認: 表在性の浅い溝を誤ってポケット認定してしまう(体積・封鎖度の評価が必要)。
実務的な次の一手
可視化確認: 既知リガンドと重ね合わせて結合部位の明確化(周辺残基名を特定)。
複数構造で再ドッキング: オープン/クローズドや異なるPDBで結果の頑健性をチェック。
短尺MD(例:50–200 ns): 活性部位の幾何指標(距離、角度、接触数)の時系列を比較。
機能仮説の明文化: どの残基・二次構造がどの動きに影響し、どう活性に波及するかを図示して計画化。
ミニアッセイ設計: 競合・非競合の判別、小分子の同時結合試験、変異体のスクリーニング計画を立てる。
必要なら、対象タンパク質名と使用した構造(PDB ID)、上位ポーズの座標を教えてください。あなたのケースに合わせて、具体的な確認ポイントとMD指標を絞り込みます。
いい質問ですね!AutoDock Vina のドッキング結果で RMSD が 0.0~0.0 と表示されているのに、自由エネルギー(binding affinity)が -4.5 kcal/mol のような値になる理由を整理します。
RMSD と自由エネルギーの違い
RMSD (Root Mean Square Deviation)
ドッキング結果の「ポーズ(pose)」が、基準構造(reference pose)とどれくらいずれているかを示す指標。
Vina では、最初のポーズ(最も良いと評価されたもの)は 基準構造そのものなので、必ず RMSD = 0.0~0.0 と表示されます。
つまり「このポーズを基準にしているのでズレはゼロ」という意味です。
自由エネルギー(binding affinity, kcal/mol)
リガンドがタンパク質の結合部位に収まったときの推定結合エネルギー。
RMSD とは独立した指標で、ポーズの「安定性」を表します。
例えば -4.5 kcal/mol なら「結合はそこそこ安定だが、強い結合ではない」という解釈になります。
なぜ「RMSD 0.0~0.0」と「-4.5 kcal/mol」が同時に出るのか
RMSD 0.0~0.0 → そのポーズが「基準」とされているため、ズレがゼロ。
自由エネルギー -4.5 kcal/mol → そのポーズの結合親和性をスコアリング関数で計算した結果。
つまり、「位置のズレがゼロ」=「基準ポーズ」であり、「自由エネルギー」=「そのポーズの安定性」なので、両方の値が同時に出るのは正常な挙動です。
補足
他のポーズでは RMSD が「基準ポーズからのズレ」として数値が出ます(例: 2.1 Å など)。
自由エネルギーはポーズごとに異なる値を持ちます。
RMSD と自由エネルギーは直接リンクしていないので、「RMSD がゼロなのにエネルギーが負」というのは自然な結果です。
要するに、最上位ポーズは「基準」なので RMSD がゼロになるが、その結合エネルギーは計算されて -4.5 kcal/mol と表示される、という仕組みです。
もしご希望なら、実際の ドッキング結果ファイル(log)を例にして解説してみましょうか?
2025年12月8日 | カテゴリー:論文/講義/発表用, AUTODOCK VINA,CLUS PRO/BIOINFORMATICS |