波動方程式

粒子の運動に伴う  ド・ブローイ波 を
ド・ブローイ波 を  表す関数(波動関数
表す関数(波動関数  と呼びます)を
と呼びます)を  Ψ(x , t )
Ψ(x , t )  としましょう.
としましょう.  シュレーディンガーは
シュレーディンガーは  粒子性の関係式 (1) を
粒子性の関係式 (1) を  考慮しながら,
考慮しながら,  波動関数
波動関数  Ψ(x , t ) の
Ψ(x , t ) の  満たすべき
満たすべき  波動方程式
波動方程式 


 を提案しました.
を提案しました.  ただし,
ただし,  プランク定数 h
プランク定数 h  の代わりに
の代わりに  それを 2π で割り算した
それを 2π で割り算した

 が使われています.
が使われています.  (アルファベットの h に
(アルファベットの h に  横棒が付いているので,
横棒が付いているので,  エッチ・バーと発音します.)
エッチ・バーと発音します.)  今後もしばしば
今後もしばしば  お目にかかります.
お目にかかります. 
 波動方程式 (3) が
波動方程式 (3) が  自由粒子 に対する
自由粒子 に対する  シュレーディンガー
シュレーディンガー  方程式 です
方程式 です
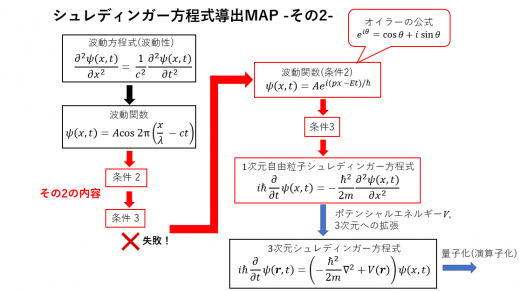
 「自由粒子の波動関数」 「自由粒子の波動関数」   シュレーディンガー方程式 シュレーディンガー方程式  (3) の最も簡単な解は (3) の最も簡単な解は     です. です.  これが 自由粒子の波動関数 これが 自由粒子の波動関数  です.このように です.このように  シュレーディンガー方程式 シュレーディンガー方程式  の解 すなわち 波動関数 の解 すなわち 波動関数  は一般に複素数 となります. は一般に複素数 となります.  これはなんだか変ですね. これはなんだか変ですね.   もともと波動関数は もともと波動関数は  ド・ブローイ波を ド・ブローイ波を  表すものと考えました. 表すものと考えました. |
 「3次元空間における 「3次元空間における  シュレーディンガー方程式」 シュレーディンガー方程式」 現実的な問題に対しては 現実的な問題に対しては  (7) 式の (7) 式の  シュレーディンガー方程式を シュレーディンガー方程式を  3次元空間に 3次元空間に  拡張しなければなりません. 拡張しなければなりません.  この場合の力のポテンシャルは この場合の力のポテンシャルは  座標 ( x, y, 座標 ( x, y,  z ) の z ) の  関数であり, 関数であり,  波動関数は 波動関数は  変数 ( x, y, 変数 ( x, y,  z, t ) z, t )  の関数となります.そして の関数となります.そして  シュレーディンガー方程式は シュレーディンガー方程式は     と書かれます. と書かれます. |
 「波動関数の確率解釈」 「波動関数の確率解釈」   下図 のように 下図 のように  3次元空間の中で,座標 3次元空間の中で,座標  (x , y , z ) (x , y , z )  の点の近傍の3辺の長さが の点の近傍の3辺の長さが  dx , dy , dz の dx , dy , dz の  微小体積 (直方体) 微小体積 (直方体)  dV = dx dy dz dV = dx dy dz  を考えます. を考えます.  時刻 t において, 時刻 t において,  この微小体積の中に この微小体積の中に  粒子が見出される確率 粒子が見出される確率  すなわち すなわち  粒子の "存在確率" を 粒子の "存在確率" を  P (x , y , P (x , y ,  z , t ) dx dy dz z , t ) dx dy dz  としましょう. としましょう.  P (x , y , P (x , y ,  z , t ) z , t )  は 点 は 点  (x , y , z ) (x , y , z )  の近傍の単位体積あたりの の近傍の単位体積あたりの  確率ですから, 確率ですから,  しばしば確率密度 しばしば確率密度  と呼ばれます. と呼ばれます.  |
 [注意] [注意] 上で 粒子の "存在確率" 上で 粒子の "存在確率"  という言葉を用いました. という言葉を用いました.  しかし,これは,例えば電子が しかし,これは,例えば電子が  常に 粒子 の形で, 常に 粒子 の形で,  粒子 の姿をして存在し, 粒子 の姿をして存在し,  ただその運動が ただその運動が  確率的である, 確率的である,  ということを ということを  意味するものでは 意味するものでは  ありません. ありません.  電子はあくまで 電子はあくまで  「粒子」 と 「波動」 の 「粒子」 と 「波動」 の  両方の性質をもった 両方の性質をもった  存在であり, 存在であり,  「粒子」だけの性質 「粒子」だけの性質  を持つわけでは を持つわけでは  ありません. ありません.  ここで言う ここで言う  "存在確率" とは, "存在確率" とは,  「粒子」を観測したとき 「粒子」を観測したとき  見出される確率 見出される確率  を意味します. を意味します.  誤解を避けるため 誤解を避けるため  "引用符" で "引用符" で  囲んでおきます. 囲んでおきます.  |
   ボルンの確率解釈は, ボルンの確率解釈は,  「粒子の "存在確率"の 「粒子の "存在確率"の  確率密度は 確率密度は  波動関数の 波動関数の  絶対値の2乗に等しい」 絶対値の2乗に等しい」  と主張しています. と主張しています.  すなわち,上図 の すなわち,上図 の  微小体積 dV 微小体積 dV  内に粒子が見出される確率は 内に粒子が見出される確率は     であると考えます. であると考えます.  波動関数 波動関数  Ψ(x , y , z , Ψ(x , y , z ,  t ) そのものは t ) そのものは  一般には 一般には  複素数の値ですが, 複素数の値ですが,  その絶対値の2乗を その絶対値の2乗を  とりますから, とりますから,  "存在確率"は常に "存在確率"は常に  正 (または 0) 正 (または 0)  となって,困ることは となって,困ることは  起きません. 起きません.  |
 「波動関数の規格化」 「波動関数の規格化」  |
 任意の時刻 t において, 任意の時刻 t において,  粒子は空間のどこかに 粒子は空間のどこかに  存在するはずですから, 存在するはずですから,  (1) 式の (1) 式の  粒子の "存在確率"を 粒子の "存在確率"を  全空間にわたって 全空間にわたって  積分すると, 積分すると,  すなわち全確率を すなわち全確率を  計算すると, 計算すると,  100% になるはずです. 100% になるはずです.  つまり つまり  波動関数 波動関数  Ψ(x , y , z , Ψ(x , y , z ,  t ) は t ) は  規格化の条件 規格化の条件     を満たすように を満たすように  なっていなければ なっていなければ  なりません.単に シュレーディンガー方程式 なりません.単に シュレーディンガー方程式  の解を求めただけでは の解を求めただけでは  規格化の条件 (2) を 規格化の条件 (2) を  満たしているとは 満たしているとは  限りません. 限りません. シュレーディンガー方程式の シュレーディンガー方程式の  ある1つの解 ある1つの解  Φ(x , y , z , Φ(x , y , z ,  t ) に,0 でない t ) に,0 でない  任意の定数 C を 任意の定数 C を  掛け算した Ψ = C Φ も 掛け算した Ψ = C Φ も  同じ 同じ  シュレーディンガー方程式の シュレーディンガー方程式の  解ですから, 解ですから,  この定数 C を この定数 C を  うまく調整すれば, うまく調整すれば,  結果の波動関数 Ψ が 結果の波動関数 Ψ が  (2) 式を満たすようにすることが (2) 式を満たすようにすることが  できます. できます.  この操作を この操作を  波動関数の規格化 波動関数の規格化  と呼び,掛けるべき と呼び,掛けるべき  定数 C を 定数 C を  規格化定数 規格化定数  と呼びます. と呼びます.  規格化定数が 規格化定数が     と書かれることは と書かれることは  容易にわかります. 容易にわかります.  |

2024年8月15日 | カテゴリー:自然科学的基礎知識//物理学、統計学、有機化学、数学、英語 |








